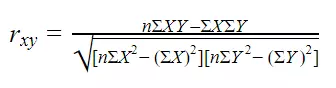Effect Size in Statistics: What it is and How to Calculate it?

Whenever changes are made in the curriculum or teaching method in a Chemistry or Physics class, we often want to assess and evaluate these changes to see their effectiveness. Although the term normalized gain is used in the science domain to measure the pre and post-modifications, it is more common in social sciences to report effect sizes than gains.

Can you guess what an effect size could possibly mean now?

What is an Effect Size?

Therefore, an effect size in statistics is measuring how important the difference between group means and the relationship between different variables. While data analysts often focus on the statistical significance with the help of p-values, the effect size determines the practical significance of the results.

Statistical significance is defined as the degree to which the null hypothesis is plausible in comparison to the acceptable level of ambiguity regarding the true answer. On the other hand, practical significance describes whether the research finding is significant enough to be meaningful in the real world. It is demonstrated by the experiment’s or study’s effect size.

A small effect size depicts that the difference between the variables is not important, while a larger effect size means that the difference is significant. It regulates the average raw gain of a population by the standard deviation of individuals’ raw scores, giving you an idea of how much the pre-and post-test scores differ.

The question is, why do we need effect size when we can work it out with statistical significance?

Let’s find out that!

Why is an Effect Size Important?

We do know that when the p-value is larger than the alpha level selected, any observed difference can be explained by sampling variability. Now, when the sample is sufficiently huge, a statistical test will always show a significant difference, regardless of how trivial the effect is in the real world. This is not the same with effect size. An effect size is not dependent on the sample size. Therefore, only reporting the p-value is not adequate for students and readers to fully comprehend the study results.

Here is an example to help you understand why the p-value is not enough to analyze outcomes:

Let’s say a sample size is 20,000, which means the p-value can be found even if the difference in results between variables or groups is trivial. The level of significance does not predict the size of the effect on its own. In contrast to significance tests, the effect size is not affected by sample size. On the contrary, statistical significance is determined by both the sample size and the effect size. As a result of their reliance on sample size, P values are thought to be confounded. A statistically significant result does not always imply that a large sample size was used.

Now that we know how vital effect size in statistics is, it time to understand how to calculate it.

How to Calculate an Effect Size?

Though there are many ways to calculate the effect size, we will only discuss the most common ones. These include the Cohen’s d and Pearson’s r methods.

Cohen’s d

The Cohen’s d method is designed to find the comparison between two means. For instance, it can be used to accompany the reporting of ANOVA and t-test results. It is also of great value in meta-analysis.

In order to find the standardized mean difference between two groups, first, subtract the mean of one group from the other and then divide the result by SD or the standard deviation of the population from which the sample was taken.

Cohen’s Effect Size Formula:

A d of 2 indicates that the two groups differ by 2 standard deviations, a d of 3 shows they differ by 3 standard deviations, a d of 4 indicates they differ by 4 standard deviations, etc.

If you remember z-scores from the previous blogs, you might notice that standard deviations and z-scores are equivalent. In other words,

1 z-score= I standard deviation

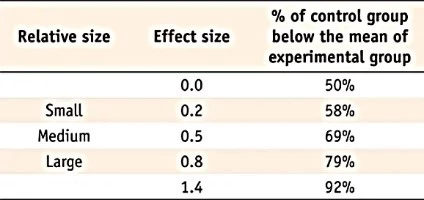
Cohen proposed that d = 0.2 represents a ‘small’ effect size, 0.5 a ‘medium’ effect size, while 0.8 a ‘large’ effect size. This means that if the difference between the means of two groups is less than 0.2 standard deviations, the difference is insignificant, even if statistically important.

Pearson’s r

Pearson’s r technique, also known as the correlation coefficient, finds out the extent of the linear relationship between two variables. You might not want to use the formula of this parameter of effect size as the formula is really complicated.

So, then how to use this parameter of effect size?

There are a lot of online statistical software to calculate the Pearson’s r from raw data accurately, so you do not need to struggle.

Where,

r_xy is the strength of the correlation between variables x and y

N is the sample size

∑ is the sum of what follows

X is every x-variable value

Y is every y-variable value

XY is the product of each x-variable score times the corresponding y-variable score

Pearson’s r is a unit-free standardized scale for measuring correlations between variables. The powers of all correlations with each other can be directly compared.

Pearson’s r, like Cohen’s d, can only be used for ratio or interval variables. For ordinal or nominal variables, other measures of effect size must be used.

FAQs About Effect Size in Statistics