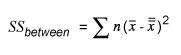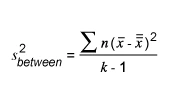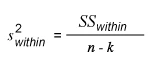Everything You Need to Know About ANOVA
Published by at September 2nd, 2021 , Revised On February 9, 2023
In the statistical analysis, some of the most questions that we face are: What are the hypothesis testing techniques, how do they work, and how(if) the processes influence variables? Also, most questions are raised related to ANOVA, as it is the most commonly used hypothesis testing technique. If you have the same or related questions in your mind, you do not need to get your teeth into finding the answers, as this article offers you a brief explanation.
Definition:
ANOVA is abbreviated as Analysis of Variance, a very useful statistical test first developed by Ronald Fisher in 1918. As the name suggests, the ANOVA test is a statistical test about finding out the variance in the means of two or more independent groups. Therefore, most statisticians firmly believe that it should be renamed to the analysis of the means instead of variance. Anyhow, the technique of ANOVA helps in identifying how independent variables affect dependent variables. This process, in turn, helps to figure out whether you should reject a null hypothesis or accept the alternate hypothesis. In simple words, ANOVA helps in finding out if the results of a research or experiment are significant or not.
Tidbit:
Independent groups:
The independent groups are the groups in statistics that include items that do not provide information about the items of other groups. These groups are not related directly or indirectly to other groups. For example, a sample of people offered with an active drug and the sample of people offered with an inactive drug are independent groups.
Dependent groups:
The dependent groups are those groups whose items are related to the items of other groups and that they provide information about them. For example, the sample of people offered an active drug, and a sample of the same people given an inactive drug are dependent.
How does it work?
The ANOVA works by analyzing the difference between the variance within the groups. The difference between means is called variance. And the variance among independent groups is called the between-groups variance. The variance between the mean of groups is calculated in the same manner as it calculated for a set of data in standard deviation. A ratio is formed between differences in the means of groups and error variance. The greater the difference between the means, the greater is the variance. If the ratio is large, the difference between groups is greater than the error. If the ratio is extremely large, the null hypothesis thus can be rejected.
Tidbit:
Null Hypothesis: A null hypothesis is a type of hypothesis that suggests that there is no difference between specific characteristics of a population.
How to use ANOVA:
Step no. 1: Find the variance between:
- Find the sum of squares between with the formula:
- Now find the variance between with the formula:
Step no.2: Find the variance within:
Step no.3: Find the ratio of the variance between and variance within:
Finally, you can find the ratio as:
Examples of ANOVA:
You can use ANOVA in a wide range of fields to find the variance in respective attributes. Some of the examples are as below:
Example no.1: Business
A company can use ANOVA to measure the success and for the comparison of different marketing techniques. In businesses where marketing and advertising are the prime focus, this testing technique can pinpoint one of the most useful strategies.
Example number 2: Medicine
Suppose there are three patients who have been suffering from the same disease. All three of them are given different medicines which say that they cure the disease. In such a scenario, the ANOVA technique can be used to identify the most effective medicine for curing the disease.
Example no. 3: Education
Suppose there are five students of grade 3 who study in different schools. You can use the ANOVA method to determine if all the students are similar or different.
Assumptions of ANOVA:
To understand the assumptions of the ANOVA, let us briefly go through the parametric test assumptions as they resemble each other. The primary assumptions made about data before applying parametric tests are:
- Data in each comparison show a Normal Distribution.
- Data in each comparison show a similar degree of homogeneity of variance or homoscedasticity.
Now, the assumptions of the ANOVA test are:
- The values of the dependent variable show a normal distribution.
- The data shows homogeneity of variance. It means that the data in each group being compared show similar variations. In the case of different variances, the ANOVA is not applicable to the data.
- An additional assumption is that the data must be collected through a statistically valid method. But if the data fails to comply with this assumption, and you need to control data, you can use ANOVA with blocking variables. A blocking variable is a variable that affects the experimental outcome, but itself is not of primary interest to the experimenter. These are included in the experiments to reduce the effect of nuisance factors.
Types of ANOVA:
1. One-way ANOVA test:
The one way ANOVA test is the most popular Analysis of Variance technique. As the name implies, the one-way ANOVA is unidirectional; it evaluates the impact of one factor. In this kind of ANOVA, only one independent variable is considered, but there is more than one level of the independent variable. It divides individuals into two or more levels. However, this is a one-way procedure as it contains one independent variable.
It compares two or more independent groups to find out whether there are statistically significant differences between the means of the groups. It is a parametric test, meaning that it checks that data comes from a population that can be modelled by a probability distribution that has fixed parameters.
One-way ANOVA test is also known as One-factor ANOVA, One-way analysis of variance, or Between subjects ANOVA. The variables used in the one-way ANOVA test include:
- Dependent variables
- Independent variables
- Active variable.
- Attribute variable
Example:
You can use a one-way ANOVA model when you have an independent variable with sub-levels and one quantitative dependent variable. For example, one-way ANOVA can be used to find the difference in hours of sleep of low, medium, and high social media consumers. Social media usage is an independent variable with sub-levels as low, medium, and high in this scenario. At the same time, the time of sleep is a dependable quantitative variable.
2. Two-way ANOVA test:
The two-way ANOVA test is another kind of ANOVA test that is used to analyze the effect of two independent variables on a continuous outcome variable. It estimates how the mean of the variables changes with the changes in the levels of categorical independent variables.
Unlike the one-way ANOVA, the two-way ANOVA test examines the effect of the independent variables on the outcome and the relationship to the outcome as well.
You can use a two-way ANOVA test when you have the data on the dependent variable at different levels of two categorical independent variables. You can use it to know how two independent variables together affect a dependent variable.
Example:
Suppose you want to analyze the IQ level of boys and girls of different regions, you can use a two-way ANOVA test. In this circumstance, Gender is one categorical variable, and location is another categorical variable. The dependent variable is IQ that must be at a continuous level.
Tidbit:
Categorical variable:
In statistics, a categorical variable is a kind of variable that has two or more categories. For example, hair colour is a categorical variable that has multiple categories as black, blonde, brown, etc.
3. Factorial ANOVA:
Factorial ANOVA is an umbrella term that covers many ANOVA tests, and two-way ANOVA is one of them. It is a procedure that helps explore the impact of two or more independent variables on a dependent variable.
FAQs About ANOVA
ANOVA is abbreviated as Analysis of Variance, which finds out the variance in means of two or more independent groups. Therefore, most statisticians firmly believe that it should be renamed to the analysis of the means. Anyhow, the technique of ANOVA helps in identifying how independent variables affect dependent variables. This process, in turn, helps to figure out whether you should reject a null hypothesis or accept the alternate hypothesis. In simple words, ANOVA helps in finding out if the results of a research or experiment are significant or not.
• The values of the dependent variable show a normal distribution.
• The data shows homogeneity of variance. It means that the data in each group being compared show similar variations. In the case of different variances, the ANOVA is not applicable to the data.
• An additional assumption is that the data must be collected through a statistically valid method. But if the data fails to comply with this assumption, and you need to control data, you can use ANOVA with blocking variables. A blocking variable is a variable that affects the experimental outcome, but itself is not of primary interest to the experimenter. These are included in the experiments to reduce the effect of nuisance factors.
There are mainly two types of ANOVA test:
One-way and two way ANOVA test
The one way ANOVA test is the most popular Analysis of Variance technique. As the name implies, the one-way ANOVA is a unidirectional ANOVA; it evaluates the impact of one factor. In this kind of ANOVA, only one independent variable is considered, but there is more than one level of the independent variable. It divides individuals into two or more levels. However, this is a one-way procedure as it contains one independent variable.
The two-way ANOVA test is another kind of ANOVA test that is used to analyze the effect of two independent variables on a continuous outcome variable. It estimates how the mean of the variables changes with the changes in the levels of categorical independent variables.
Unlike the one-way ANOVA, the two-way ANOVA test examines the effect of the independent variables on the outcome and the relationship to the outcome as well.