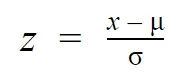Standard Normal Distribution – A Comprehensive Guide

The standard normal distribution is a special kind of normal distribution where the mean is 0, and the standard deviation is 1. It is also known as z-distribution, which is a normal distribution of standardised values called z-scores. A z-score, also known as a standard score, tells you how far a data point is from the mean. Technically, the z-score measures how many standard deviations below or above the population mean.

For example, if the mean of a normal distribution is six and the standard deviation is three, the value of twelve is two standard deviations above the mean. You can calculate it by:

x = μ + (z) (σ) = 6 + (2)(3) = 12

In the case of standard deviation, the mean is zero, and the standard deviation is one. When you put the figures in the formula, the result:

x = μ + (z) (σ) = 0 + (1) (σ) = σ

Standard Normal Distribution

Difference Between a Standard Normal Distribution and Normal Distribution

The standard normal distribution, like other normal distributions, is symmetrically distributed, making a bell-shaped curve. So, the standard normal distribution is a normal distribution with mean=0 and standard derivation= 1. While normal distribution can have a mean and standard deviation, the standard normal distribution has a fixed mean and standard deviation.
In other words, when plotted on a graph, it can be said that the curve of a normal distribution is a kind of standard normal distribution that has been moved horizontally right or left. You have learned in the normal distribution that the mean and standard deviation are the parameters; changing the values either stretches or squeezes the curve.
Changing the value of the standard distribution from 1 to any number, for example, 2, can turn a standard normal distribution into a normal distribution. You can use the probabilities of the standard normal distribution to find probabilities for a normal distribution, as standard one can represent any normal distribution. However, it is essential to note that you have to be certain about the

In this way, standard normal distribution and normal distribution are linked to each other.

Brain Booster: What is a Normal Distribution? 

A normal distribution, also known as Gaussian distribution or probability density distribution, is a probability distribution that is symmetric about its mean, with all data points near the mean. When plotted on a graph, the normal distribution looks like what is popularly called a bell curve. Bell, however, is not a technical term; it is used for convenience in the series.

Properties of Standard Normal Distribution

The properties of the standard normal distribution have somehow similar and somehow different properties than the normal distribution.

• Like the normal distribution, the total area under the standard normal curve is 1.
• The standard normal curve extends indefinitely in both directions horizontally.
• A standard normal curve is bell-shaped.

How to Standardise a Normal Distribution?

You should carry out a process on normal distribution that has mean= 0 and standard deviation= 1 to make it standard normal distribution. Standardizing the normal distribution makes it easier to calculate the probability of values. It also helps to compare different data sets with different means and standard deviations. The data points in the standard distribution are referred to as Z-scores. As mentioned earlier, the z-score tells you how many standard deviations away a value lies. Converting a normal distribution into the standard normal distribution helps you to:

• Compare scores on different distributions and with different means and standard deviations.
• Find the probability of observations in a distribution.
• Find the probability that the sample mean significantly differs from a known population mean.

Conditions

• If the z-score is positive, the x-value is greater than the mean.
• If the z-score is negative, the x-value is less than the mean.
• If the z-score is zero, the x-value is equal to the mean.

Calculating the z-score:

X= individual value

μ = mean

σ = standard deviation

Process of Standardisation

You have to standardise the normal distribution in a way that its mean becomes 0 and the standard deviation becomes 1.

For example, you have a normally distributed set of numbers 2, 3, 3, 4, 4, 4, 5, 5, 6.

The mean is 4, and the standard deviation is 1.15.

Now, subtract all the individual values from the mean. It will result in a data set of -2,-1,-1, 0, 0, 0, 1, 1, and 2.

Now, their mean is 0, but we have to work on the standard deviation, which is 1.15.

Divide each data point by 1.15.

We will get a data set of: -1.73, -0.86, -0.86, 0, 0, 0, 0.86, 0.86, 1.73

The standard deviation of this set is 1.

Example: You score 200 on your math test. The test has a mean of 150 and a standard deviation of 25. Assuming a normal distribution, what would be your z-score?

Solution:

We will use the formula to find a z-score.

By putting the values:

Z= 200-150/25

Z= 2

The Z-Score tells you how many standard deviations away your score is from the mean. In this example, it is 2 standards deviations above the mean.