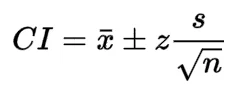Explaining Confidence Intervals

Let’s say you want to find out how many children drop out of school before they turn 18 in a certain town. You could survey every child in the town, but that wouldn’t be so plausible, would it? It would be expensive and nearly impossible for you to survey each one of them. To save time and money, you would probably survey a smaller group of children. However, there still may be chances that your findings are different compared to if you had surveyed the entire population. This means that each time you repeat the survey, you would likely get slightly different results.

Commonly, when researchers survey a small group and present an estimate for a large population, they use confidence intervals (CI).

What Are Confidence Intervals?

A concept probably everyone learns about in their first statistics class, however, still very few know their importance. Confidence intervals – as the name – tell us how confident we are in our results. It’s a range of values, bounded above and below the statistical mean, that is likely to be where our true value lies. It measures the degree of certainty and uncertainty in a sample and is usually measured using statistical analysis methods, such as the T-test. Because confidence intervals represent the range of values that are likely if we were to repeat the experiment, they are important to consider when generalizing results. When talking about confidence intervals, it is important to know about confidence levels since they are inter-connected to each other.

Confidence Levels – What Are They?

Confidence levels are expressed in percentages. Of course, we can never be 100% sure that our results can be repeated with any survey or experiment. So in statistics, if we’re 95% sure that our results could be repeated, it is considered statistically sound. This means that if we conduct our experiment repeatedly, 95% of the time, our results will match the results we get from a population. In simple words, our statistics will be sound. Similarly, if our confidence level is 0%, it would mean that we have no faith that if we were to repeat the test, we’d get the same results.

Let’s say you’re surveying a group of families to see how many times they order fast food in a year. You test your statistics at the 98 percent confidence level and get a confidence interval of 50-100. This means that you think they order fast food between 50 and 100 times a year. You’re super confident about this, too, because your results are sound statistically (98% is a pretty high level).

Factors That Affect Confidence Intervals

• Sample Size: The smaller your sample size, the less confident you can be about your results. The smaller your sample size, the larger your confidence interval.
• Percentage: The accuracy of your results also depends on the percentage of the sample that picks a certain answer. For example, if 98% of people in a sample are dog lovers and 2% of them are cat lovers, the chances of error are less, irrespective of your sample size. However, if in a sample, 51% are dog lovers and 49% of them are cat lovers, there is a greater chance of error.

Why do Researchers Use Confidence Intervals?

It is nearly impossible to study the entire population to formulate a result, so researchers use a smaller sample of the population. A confidence interval is simply a way for them to measure how well the sample reflects the population they are studying.

Here’s how Confidence levels are Calculated

For a normal distribution/ z-distribution

Sample problem:

Construct a 95% confidence interval when the sample mean weight of children in an elementary school was 104 pounds, with a standard deviation of 1.2. There are 5 samples in this experiment.

Solution:

Using the following formula

Where

• CI = the confidence interval
• X̄ = the population mean
• Z* = the critical value of the z-distribution
• σ = the population standard deviation
• √n = the square root of the population size

Step 1 To find the α level, we’ll subtract 1 from the confidence level we have and then multiply it by 2. This represents the area in one tail.

(1-0.95)2

= 0.025

Step 2 Next, we’ll subtract the answer in step 1 from 1 and then look up that area in the middle of the z-table to get the z-score.

1 – 0.025=0.975

Z-score=1.96

Step 3 Next, we’ll plug in this value in the formula.

z* σ / (√n)

= 1.96 * 1.2/√(5)

= 1.96 * 0.5357

= 1.05

Step 4 For the lower end of the range, we’ll subtract step 3 from the mean. Therefore, we’ll get,

104 – 1.05 = 102.95

Step 5 For the upper end of the range, we’ll add step 3 to the mean. Therefore, we’ll get,

104 + 1.05 = 105.05

The CI is (102.95,105.05)

And that’s how you find a confidence interval for a normal/ z distribution!

For a T-Distribution in a Sample

Sample problem:

A group of 10 children in a college had a mean weight of 150 pounds. The sample standard deviation was 20 pounds. Deduce the confidence interval for the true mean weight of all the college students. Find a 95% CI.

Solution:

Step 1: Subtract 1 from your sample size. In this example, it’s 10.

10 – 1 = 9. This gives you the degree of freedom, which we’ll require in Step 3 of this solution.

Step 2: Next, we’ll subtract the confidence level from 1, then divide by two.

(1 – .95) / 2 = .025

Step 3: We’ll look up the answers to step 1 and 2 in the t-distribution table. For 9 degrees of freedom (df) and α = 0.025, the result is 2.262.

Step 4: Dividing this given standard deviation by the square root of the sample size, we’ll get,

20 / √(10) = 6.235

Step 5: We’ll then multiply step 3 by step 4.

2.262 × 6.235 = 14.307

Step 6: For the lower end of the range, we’ll subtract step 5 from the sample mean.

150 – 14.307 = 135.69

Step 7: For the upper end of the range, we’ll add step 5 to the sample mean.

150 + 14.307 = 164.307

(135.69,164.307)

And that’s how to find the confidence interval for a!