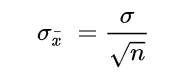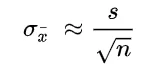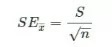Standard Error in Research – A Complete Guide

Standard error, abbreviated as SE, is a mathematical tool used to assess the variability in statistics. It is the approximate standard deviation of a statistical sample population for estimating the accuracy, efficiency, and consistency of a sample. In simpler words, it measures how accurately a sampling distribution depicts a population. It is used in various fields from mathematics to economics and statistics, but it is of utmost importance in econometrics, where it is utilized by researchers for hypothesis testing and performing regression analyses.

The standard error can sound all Greek to most students, even researchers, but with the help of this guide, you will undoubtedly get the most out of it.

Understanding SE in Research

The term usually refers to the standard deviation of different sample statistics in research, such as the mean or median. For instance, the standard error of the mean reflects the standard deviation of the distribution of sample means gathered from a sample. If the standard error here is smaller, there is a good chance of the sample being more representative of the entire population. Or, we can say,

↓Standard Error = ↑Sample Representative of Population

How to Calculate the Standard Error of Mean (SEM)?

It can be measured with the help of this formula:

What the signs represents:

• σ – Population standard deviation
• n – Sample size, i.e., the number of observations in the sample

Other commonly used measures include:

• Standard error of the variance
• Standard error of a regression coefficient
• Standard error of the median

Sometimes statistics are ignorant of the population standard deviation, and in such cases, researchers use the sample standard deviation as an alternative. The formula for that is:

In which:

• ‘s’ is Sample Standard Deviation
• ‘n’ is Sample Size, i.e., the number of observations in the sample

We have come this far, but some might still mix the two terms: standard deviation and standard error. If so, let our things a bit before moving forward.

Standard Error vs. Standard Deviation

Firstly, the standard deviation is the absolute measure of dispersion in a series and is used to evaluate the amount of variation on both sides of the mean. Standard error, on the contrary, is used to assess the accuracy of an estimate. As simple as that!

Secondly, the standard deviation is descriptive, while standard error is always inferential.

Thirdly, the standard deviation is the distribution of concerning normal curve when it comes to distribution, while standard error shows the distribution of an estimate concerning the normal curve.

Lastly, there is a massive difference in their formulae.

Standard Error

Why is Standard Error Important?

When a researcher extracts a sample of observation from a population, the sample mean can be calculated, which estimates the population mean. The population mean would differ from the actual population mean. The researcher can thus identify the extent of the difference or variation by using standard error.

Although, with the help of probability sampling, you can collect data that might represent the whole popular as elements are randomly selected here. However, even then, there is an excellent probability of sampling error with this method as well. Why? Because a sample can never match the entire population a hundred percent, and there always is room for mistakes.

By calculating the standard error, you can estimate the sample’s representative for the whole population and draw conclusions accordingly.

Pro Tip:

If you want to minimize the sampling bias, make sure to take a larger random sample. By increasing the sample size, you can decrease the standard error.

This brings us to the next heading, which is the relationship of sampling size and the standard error of the mean.

Sample Size and Standard Error of the Mean

We just discussed how both these terms are inversely proportional to each other. Meaning, if the value of one of these increases, the other will decrease. Here is an example to show how.

Let’s suppose 60 students in a Biology test have different scores. You take two samples, A and B, and some 30 observations. It is quite rational to think that the average marks in the second sample, which is B, will be much closer to the average marks of the entire population (50 students) than the first sample group A.

So, we can say that the standard error of the mean in sample B might be might smaller than the first. The standard error of the mean here would approach zero with the ascending number of observations as the sample becomes more and more representative of the whole population. The sample mean will thus approach the actual population mean.

We know that according to the formula of the standard error of the mean that if it increases, the sample size decreases. This means if the sample size is increased, the standard error will automatically decrease.

Calculating the Standard Error

Now comes the fun part: calculations!

Follow these simple steps to get the standard error.

Step 1: Figure out the number of measurements you require and determine the sample mean which is the average of all measurements. So, you need the value of ‘n’ and ‘μ.’

Step 2: Now check how much each measurements differs from the mean.

Step 3: Next is squaring all the deviations and adding them together. The formula is Σ(xi – μ)²

Step 4: The value you got from the above equation is then divided by one less than the total measurements. Or (n-1)

Step 5: Then find the standard deviation (σ) which you can get by the square root of the obtained value.

Step 6: Lastly, divide the standard deviation by the square root of the measurements.

Can you solve Standard Error now?

Here is a question for you.

Q: Find the standard error of the given data:

Y=10, 20, 24, 29, 40

FAQs About Standard Error