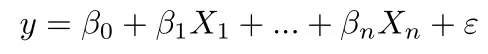Multiple Linear Regression

What Multiple Linear Regression (MLR) Means

Just as a simple linear regression model represents a linear relationship between an independent and dependent variable, so does a multiple linear regression. The only difference is that in the latter, there are two (or more) independent variables and one dependent variable. 

So, in statistical analysis, a multiple linear regression model is used when there are two or more independent variables—x1 and x2—that are predicted to change another variable, y. The relationship correlation can be such that when one or all independent variables increase/decrease, the dependent variable also increases/decreases. 

In other words, in MLR, some explanatory or predictive variables are used to account for the chance in a regular response or variable. 

The following examples can be used to see how that might happen statistically:

Examples

• Effects of diet on an individual’s height and weight (height and weight = independent variables; diet = dependent variables). 
• Change in mental well-being based on monthly income and work environment in a specific area for a certain group of people (monthly income and work environment = independent variables; mental well-being = dependent variable).

Pre-Suppositions of MLR

They are the same assumptions that guide the formation of a simple linear regression model. Even in the case of MLP, the statistical data of research qualifies to be represented through an MLR model when it meets these criteria:

1. Normality: Data is normally distributed.
2. Linearity: The relationship between the two variables is linear; that is, one decreases, and so does the other, or vice versa. 
3. Homogeneity of variance, aka homoscedasticity: Values of the independent variable aren’t much affected/altered by the size of the error in predictions, no matter the size of that error.
4. Independence of observations: Trust-worthy, valid, and accurate methods have been used to collect data; the data aren’t connected in some hidden way. However, in the case of MLR, sometimes both independent variables are found to be closely connected in some subtle way. For instance, it might turn out that temperate and rainfall both closely correspond to crop growth.
5. There needs to be two or more independent variables, which can either be continuous (an interval or ratio variable) or categorical (an ordinal or nominal variable). For instance, gender (containing 2 groups: male and female) is a good example of a nominal variable. 

When that happens, a researcher ought to consider only one out of two such independent variables. Even though it’s a multiple linear regression, bear in mind, it’s still linear. The plotted line has to be linear, and the inclusion of one such variable ensures that.

How to Form SLR Model Using Formula – Method 1

Just as there’s a formula for SLR, there’s one for MLR, too, and that is shown below. After organizing your data into respective categories (independent and dependent variables, their coefficients, intercepts, etc), apply this formula to calculate MLR for this data set:

Where:

• y = predicted value of the dependent variable  
• x1 = any given value of one independent variable 
• x2 = any given value of the second independent variable
• B0 = the y-intercept that is, the value of y when every other parameter is set to 0
• B1x1= regression coefficient (B1) of one independent variable (x1) that is, the extent to which y is predicted to change as x1 changes
• … = x with a subscript number depending on the number of an independent variable there is (2, 3, 4, … )
• Bnxn = regression coefficient of the last independent variable (n can be any number, depending on the number of variables it is)
• B0 = intercept that is, predicted value of y when x = 0 or, in other words, the point where an estimated regression line will cross the y-axis
• B1 = regression coefficient that is, the extent to which y is predicted to change as x changes
• e = error of estimate that is, how much the regression coefficient is expected to vary.

How to Form SLR Model by Hand- Method 2

Once data has been collected, it has to be sorted, and the following steps can be applied to calculate MLR by hand:

Step # 1 – Make columns for y, x1, x2 and input their values accordingly.

Step # 2 – Square x1 and x2.

Step # 3 – multiply both x1 and x2 with the dependent variable y. That will be X1y and X2y.

Step # 4 – Multiple both independent variables together, and that will be x1x2.

Step # 5 – Calculate the sum of regressions.

Step # 6 – Calculate b0, b1, and b2, where the formula to calculate

• b1 is [(Σx22)(Σx1y)  – (Σx1x2)(Σx2y)]  / [(Σx12) (Σx22) – (Σx1x2)2]
• b2 is [(Σx12)(Σx2y)  – (Σx1x2)(Σx1y)]  / [(Σx12) (Σx22) – (Σx1x2)2]
• b0 is: y – b1X1 – b2X2

Step # 7 – Insert b0, b1, and b2 in the following multiple linear regression equation:

ŷ = b0 + b1*x1 + b2*x2

To better understand all these steps in action, some examples using the above steps, as well as other MLR examples, will help.

How to Form SLR Model Using Excel and SPSS

These days, almost everyone might be using Excel, SPSS, or some other online tool and software to calculate MLR. They perform all the calculations and plot a linear plot representing the data at hand.

Interpreting and Representing Data through MLR

In other words, one might interpret data represented otherwise graphically in MLR as something like:

(Related to the example mentioned above regarding rainfall, temperate and crop growth): “A 2% increase was observed in crop growth for every 0.5% increase in rainfall and 1% decrease in crop growth for every 2% increase in temperature.”

The point is to depict the relationship both independent variables have on the single dependent variable, separately.

Frequently Asked Questions