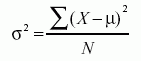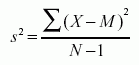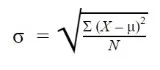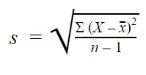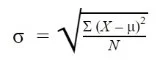Measures of Variability
Published by at August 31st, 2021 , Revised On April 10, 2023
As we discussed in the earlier guides, variability refers to how spread out data points are from the center of the distribution. Measures of variability in statistics is a summary explaining the proportions of fluctuation in the dataset. While a measure of tendency reflects the typical value, the measure of variability shows how far away data points tend to fall. If the data points fall far from the center of the distribution, we call it a high dispersion, and if the data points cluster tightly around the center, it is low dispersion.
In this guide, we will see what some measures of variability in statistics are and shed light on their significance.
What are Measures of Variability?
There are four common measures of variability. These are:
- The Range
- Interquartile Range
- Variance
- Standard Deviation
Let’s discuss each of these in detail.
The Range
Range is the simplest to understand and undoubtedly the most commonly used measure of variability. The range of a dataset is defined as the subtraction or difference between the largest and smallest values. For instance, if you look at the two datasets below, dataset 1 has a range of 30-48. While dataset 2 has a range of 10-42.
The two datasets clearly show that dataset 2 has a much broader range and is more variability than dataset 1.
What is the range based on?
Well, the range might be pretty simple to understand and calculate, but it is based on some factors. Firstly, it depends on the two most extreme values in a dataset, which can be susceptible to outliers. If the value of any one of these is unusually low or high, it can affect the entire range. Or, we can say, ruin it.
Secondly, the size of the datasets can also have a direct influence on the range. You will not be able to observe extreme values in general, but as you increase the sample size, there is more room for obtaining extreme values. In such cases, you draw random samples where the range increases with the increase in the sample size.
Note: It is best to only use range for comparing variability only when the samples sizes are same.
If this one is clear, let us talk about the Interquartile Range.
What data collection best suits your research?
- Find out by hiring an expert from ResearchProspect today!
- Despite how challenging the subject may be, we are here to help you.
The Interquartile Range
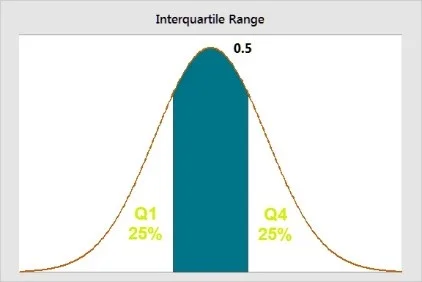
The interquartile range, frequently called IQR, is the middle half of the data. You might have guessed that already from the first half of the word ‘Interquartile.’ To better understand, let us try to visualize it. Think about the mean value that divides the dataset into equal parts. Now imagine splitting the data into quarters. There you have it!
The four parts or quarters you get here are termed quartiles in statistics, and they go from low to high. The lowest quartile is Q1, followed by Q2, Q3, and Q4. While Q1 contains the quarter of the dataset with the smallest value, Q4 has the quarter of the dataset with the highest values.
The middle half of the data, which is in between the lower and upper quartiles is thus, the interquartile range. We can also say that the interquartile range concludes 50 percent of the data points falling between Q1 and Q3.
The interquartile range in the figure above is the blue area.
Here is a solved question to help you understand the term better.
| Dataset |
| 25 |
| 42 |
| 45 |
| 69 |
If you have to find the IQR of your 4 data points, you will first see the values at Q1 and Q3.
Now, multiply the number of values in the data set, which is 4 in this case, by 0.25 for the 25th percentile. And for Q3, multiply by 0.75 (75th percentile).
Q1: 0.25 x 4=1
Q3: 0.75 x 4= 3
Q1 is the value in the first position, and Q3 is the value in the fourth position. So, Q1 is 25, and Q3 is 69. For IQR, we will subtract Q1 from Q3.
IQR= Q3-Q1
IQR= 69-25= 44
The Variance
Variance in statistics is defined as the average squared difference of values you get from the mean. Unlike the range and interquartile range, this measure of variability includes all the values in the calculation, which is done by comparing each value with the mean.
So, you first find out a set of squared differences between data points, then the mean, followed by their sum. After you sum them, you divide the answer by the total number of observations.
There are two ways or formulas for calculating the variance depending on whether you want variance for the entire population or a sample to estimate the population variance.
These formulas are:
The formula for the variance of the whole population=
Here, σ2 is the population parameter for the variance, μ is the parameter for the population mean, while N is the number of data points that include the entire population.
Formula for the variance of a sample=
Here, s2 is the sample variance, and M is the sample meanwhile N-1 in the denominator corrects for the tendency of a sample to underestimate the population variance.
Not sure which statistical tests to use for your data?
Let the experts at ResearchProspect do the daunting work for you.
Using our approach, we illustrate how to collect data, sample sizes, validity, reliability, credibility, and ethics, so you won’t have to do it all by yourself!
Standard Deviation
The last most used measure of variability is the standard deviation, which is the typical difference between each data point and the mean. If you group the values in a dataset closer together, you get a smaller standard deviation. However, when the values are far away, the standard deviation in such a case is larger. So, an increase in distance is directly proportional to the increase in the standard deviation size.
Standard deviation is the most preferred measure of variability because it uses original data units; hence, the interpretation is much easier.
Here are the six simple steps to calculate the standard deviation:
- Naming of each score and finding their mean.
- Subtracting the mean from each score for getting the deviation from it.
- Squaring each of these deviations.
- Adding up all the squared deviations.
- Now dividing the sum of the standard deviations by n-1 if it is a sample, and N if it is a population.
- Lastly, finding the square root of the number you get.
Also, these are the standard deviation formulas for sample and population:
Formula to Find the Standard Deviation of a Population
Where:
σ = population standard deviation
∑ = sum of…
X = each value
μ = population mean
N = number of values in the population
Formula to Find the Standard Deviation of a Sample
Where:
s = sample standard deviation
∑ = sum of…
X = each value
x̅ = sample mean
n = number of values in the sample
Why is Variability Important to Calculate?
Let’s try to understand the significance of variability measurement from real-life examples.
You go to college every day and try to get there for the first class, which starts at 9:00 am. Sometimes you make it to class on time, and other times, the commute takes longer than planned. Similarly, you get breakfast from your favorite café near the college and think the same dish tastes a little different each time you try it. Your office ends at 5:00 pm, and you head home at 5:10, sometimes 5:15, and so on. But, the time might vary each day depending on the kind of work you get.
So, you see, some kind of variability is always there. Nothing goes as planned, and there is no way you can change that. However, if there is too much inconsistency, will you like it? For instance, in the above examples, if you miss your classes often because you are late. Or, you do not like the breakfast you order because it is way different than it should be. Or, you head home late every day and miss out on other things. None of these are likable.
Thus, it is essential to understand that some variation can be inevitable, but issues might occur at the extremes. The same is the case here. You do not want extremes, but if they are there, you should have a way to measure them to get accurate results without deviations.
FAQs About Measures of Variability
Measures of variability in statistics is a summary explaining the proportions of fluctuation in the dataset. There are four common measures of variability. These are:
1. The Range
2. Interquartile Range
3. Variance
4. Standard Deviation
Formula to Find the Standard Deviation of Population
Where:
σ = population standard deviation
∑ = sum of…
X = each value
μ = population mean
N = number of values in the population
Formula to Find the Standard Deviation of a Sample
Where:
s = sample standard deviation
∑ = sum of…
X = each value
x̅ = sample mean
n = number of values in the sample
Central tendency reflects the typical value of data points, while measure of variability shows how far away data points tend to fall from each other.
Variance is defined as the average squared difference of values you get from the mean. Unlike the range and interquartile range, this measure of variability includes all the values in the calculation which is done by comparing each value with the mean.