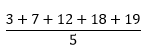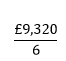A Comprehensive Guide on Mean
Published by at September 21st, 2021 , Revised On July 20, 2023
What is Mean?
Mean goes by another commonly known and used term, ‘average.’ In younger grades, students are generally taught average using simple mathematical examples. Examples like ‘calculate how much money Jane has overall if she saved up £10 every month for 6 months and the like.
Average, or mean, therefore, is the ‘central value’ in a dataset. Here, a dataset can mean a couple of numbers or other values. This central value is statistically called the central tendency. What it represents is probability. The probability that a certain value (the mean) will be achieved or reached when a couple of other values (what the mean is calculated from) are considered.
How is mean calculated?
Calculating the mean of a given set of values is simple because it involves basic maths: addition and division. To calculate the mean, one simply has to:
- Take all the values present in a dataset.
- Add them all up.
- Divide them by the total number of values present in that dataset.
What are some examples of Mean?
Following are some easy-to-understand examples of the mean from daily life:
Example #1:
Lory is a 5th-grade student. Her biology teacher wants to keep a portfolio of her student performance over the past five months. To do so, she needs to see Lory’s test grades and assign a letter grade to Lory for her test performance. However, multiple tests were conducted over the past month. So, the teacher will take out their mean.
Following a summary of Lory’s test performance over the past five months.
| Test # | Marks obtained | Marks obtained out of |
|---|---|---|
| 1 | 3 | 5 |
| 2 | 7 | 10 |
| 3 | 12 | 15 |
| 4 | 18 | 20 |
| 5 | 19 | 25 |
To calculate the mean, the teacher will perform the following calculations:
x̄ =
x̄ = 11.8
If the five tests carried a weightage of 25% in the overall course work, five tests’ marks would be out of 75, or an average of 18.75. So, Lory achieved 11.8 marks out of 18.75, as the above mean average shows.
Example #2:
Eric is an auto sales representative in an international automotive company. He wants to know how much profit he will receive if he saves £8,000 – £10,000 each month from his pay. He’ll calculate the mean profit as such:
x̄ =
x̄ = £1,553.3
This means Eric was able to save £1,553.3 per month from his savings on average.
How is mean represented?
In statistics, the mean is commonly denoted as x̄, read as ‘x bar.’ However, the Greek letter mu, μ, is also used to represent mean. Although, it should be noted, that it represents the population mean in research.
Furthermore, another Greek letter ∑, read as ‘sigma,’ is also used in some places to represent the sum of numbers. While calculating the mean, the sum of all the numbers is written in the numerator. As a short form, it can also be denoted as:
Where n stands for the total number of values, such as 6 in example #2 above. ∑n represents the average, or sum, of all the numbers in a given dataset. In both the examples both, the different values together comprise what is called a dataset (3 + 7 + 12 + 18 + 19, from example #1, for instance).
Where is the mean used?
Calculating the mean gives an idea of the overall picture of the dataset. The mean value is treated as a yardstick to compare other values.
Mean is commonly used in finance (such as for business valuation, portfolio management, etc.), statistics and other mathematical and/or related areas. It’s also used in academic research when a researcher has to calculate the mean of a population; the probability a certain type of response from a questionnaire has of being selected from different options and so on.
Did you know: Mean is also used in sports. The balling/batting average shown on a screen against players’ names is calculated using mean!
Is calculating mean important? Why or why not?
Despite its simplicity and straightforward calculations, the mean is a crucial part of any mathematical or statistical calculation.
It’s important because of a couple of reasons, including but not limited to:
- It reduces error while predicting any value in the dataset. In other words, mean given that value which produces the slightest of error from the remaining values of a dataset.
- The mean tells about when the highest value lies in a given dataset. This is especially useful if the mean is to be used for plotting a bell graph. In that case, the average value will be represented by the highest point of the bell curve.
The biggest advantage, therefore, of calculating the mean for a given dataset is that it can be used for further data representation. It also gives a straightforward idea about the dataset, which value will be the highest and where it will lie in terms of the other values in the set.
When is mean NOT calculated?
The biggest disadvantage of using mean is that it can be skewed by outliers. Outliers are either very large or very small values in a dataset. They can ‘skew’ the mean and in turn, if that mean is used to plot a bell graph, the resulting bell curve will also be skewed (not like a bell, that is).
A skewed mean is statistically called a skewed mean distribution. It occurs when the mean is too close to either one of the clusters in the data sets; it’s not central. It’s distributed in a ‘skewed’ way.
A simple example of skewed mean distribution is a dataset containing just three values: 10, 20 and 30. Their mean will be 20. This is a central measure, so it’s not skewed. However, if another value is added to the far left or far right, it will become skewed (-20, 10, 20, 30, in which case the mean will be 10, not in the centre but to the far left). Here, 10 is considered to be distributed in a skewed way because, as the following pattern shows:
-20 10 20 30
There are more values to the right of 10 than to its left. Hence, statistically speaking, this mean value of 10 is skewed to the left. If another value were added, the mean would become central again, with an equal number of values (two) on each side.
Frequently Asked Questions
They both are not as much the same as much as being two sides of the same coin. Average is a sum of all the values in a dataset divided by the total number of values. Mean is also the same, theoretically, but it can involve the sum of more than one dataset. It’s a statistical way of describing an average of a sample or dataset.
Median is the middle value of a dataset. It has to be calculated for an even number of values in a dataset, but not for odd-numbered datasets. However, the central tendency in mean always has to be calculated; it’s not a middle value but a central tendency from the OVERALL values in a dataset.