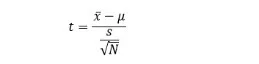T Distribution – Applications, Formulas & Properties

Confused? What differentiates t-distribution from a normal distribution? Wondering why they are used?

Fret not! You will find all this and more in this write-up.

This blog sheds light on the definition, properties, and uses of t-distribution. It also discusses t-scores and why they are used in statistics.

What is a T Distribution?

The t-distribution is the probability distribution that predicts the population parameters when the population standard deviation is unknown and the sample size is small.  The Student’s t-Distribution is another name for t-distribution. It has a lot of similarities with the normal distribution.

When the sample size increases, the t-distribution tends to look more normally distributed with the values of standard deviation and means of 1 and 0, respectively.

Quick Recap

Population: Population in the research market comprises all the members of a defined group that you generalize in order to find the results of your study. This means the exact population will always depend on the scope of your respected study.

Parameter: The measurable quality of the population is called a parameter.

Standard Deviation: It is one of the most used measures of variability, which is the typical difference between each data point and the mean. Standard deviation is the most preferred measure of variability because it uses original data units; hence, the interpretation is much easier.

Sample Size: The total number of people selected for the survey/study

What is the Formula for T-Distribution?

Keep in mind that t-distribution comprises the whole set of t values you can measure for every possible random sample and specific sample size. It is almost like the shape of a normal distribution. Normal distributions are probability bell curves where the mean is zero and the standard deviation is 1. All normal distributions are asymmetrical. However, not all asymmetrical distributions can be normal.

Suppose x has a normal distribution with a sample size ‘n’, mean ‘μ’, the sample mean x¯, and the sample standard deviation ‘s’. Here, the t variable will, thus, have student’s t-distribution with a degree of freedom, d.f = n – 1

The formula for t-distribution is:

Where,

x¯= mean of the first sample

μ = mean of the second sample

s = sample standard deviation

{N} = sample size

Properties of T Distribution

1. Similar to the standard normal distribution, the student distribution is symmetrical and bell-shaped, with a mean of 0
2. The student distribution can go from –∞ to ∞ (infinity)
3. The shape of the t-distribution varies with the change in the degrees of freedom
4. It is higher in tails and less peaked at the center, therefore it calculates a platykurtic shape
5. The variance here is always bigger than 1 and can only be defined when the degrees of freedom is ν ≥ 3 and is given as Var (t) = [ν/ν -2]
6. The standard normal distribution has a smaller dispersion as compared to a t-distribution. When the sample size gets bigger, it assumes the normal distribution. The sample size is considered big when it is n ≥ 30

Applications of the T Distribution

Find a few important applications for T distribution below:

a)   Test of Hypothesis of the Population Mean:

If the population is distributed normally, and the standard deviation is unknown, ‘t’ statistic can be measured with:

Where,

X͞ is the sample mean

? is the population mean

‘N’ is the sample size

Note: The null hypothesis is tested in order to see if there is a significant difference between ‘?’ and ‘X͞’. When the calculated t-value is greater than the table value of ‘t’ at a particular level, then the null hypothesis is not plausible. On the contrary, if the calculated value of ‘t’ is smaller than the table value of ‘t’, then the null hypothesis is plausible.

b)   Test of Hypothesis of the Difference Between Two Means:

There are two ways to test the difference between two population means whose population variances are unknown:

When variances are equal:

Here,

X͞1 and X͞2 are the sample means of sample 1 of size n1 and sample 2 of size n2

When variances are unequal:

We use the unbiased estimators S1² and S2² if the population variances are not equal.  In this case, the formula will be:

In this,

?1 and ? 2 are the two population means

c)    Hypothesis Testing of the Difference Between Two Means with Dependent Samples

Many times samples are deduced from two populations that depend on each other. That is why these samples are called dependent samples. You will notice that each observation included in one sample is associated with a particular observation in another sample. Because of this property, the test t utilized in this case is called a paired t-test.

This test is mostly used in experiments where the before and after are to be compared. Two kinds of methods are applied depending on the situation and case.

For instance, if the means of both the methods applied are equal then this statistic would be used:

This statistic is based on a t-distribution with (n-1) degrees of freedom, with d = the mean of the differences calculated as follows:

The standard deviation of differences can be calculated by the formula:

Where,

‘n’ is the number of paired observations.

T-Scores and T-Distributions

The number of standard deviations from the mean in a t-distribution is called a t-score. How to look up a t-score?

This one’s quite easy. There are online t-score calculators, so it actually is not as tedious as it might sound.

T-scores are used to find two things in statistics:

1. You can calculate the lower and upper bounds of a confidence interval when data are normally distributed
2. The p-value can also be found out for regression tests and t-tests with this

FAQs About T Distribution