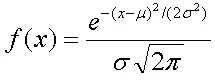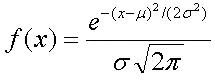What is a Normal Distribution?
A normal distribution, also known as Gaussian distribution or probability density distribution, is a probability distribution that is symmetric about its mean, with all data points near the mean. When plotted on a graph, the normal distribution looks like what is popularly called a bell curve. Bell, however, is not a technical term; it is used for the convenience in the series. There are many ways data can be distributed, for example:
- The data can be distributed more on the left.

- The data can be distributed more on the right.
- The data can be distributed symmetrically.
The method in which data is distributed with no skew is called a normal distribution. Note: Skewness, in the statistics, is asymmetry or distortion from the bell curve. Draw an imaginary line connecting the bars of a normal distribution graph. It results in the formation of a bell curve.
History of Normal Distribution:
Before the inception of normal distribution, there was error distribution. In the 17th century, Galileo noted that the errors in his measurements had a consistent distribution. He found out that the small errors occurred more often than larger errors.
It led to many hypotheses about error distributions, but it was in the 19th century that it was discovered that errors follow a normal distribution. The deductions of Galileo were further formalized by Gauss and many others, which is why a normal distribution is called a Gaussian distribution.
The name probability density distribution is a more intuitive way of understanding Gaussian distribution. According to the findings of Galileo, the probability of making a small error is greater than making a large error, so the probability is denser around the mean of the measurements.
Properties of Normal Distribution:
- Mean, median, and mode are all equal.
- The curve is symmetric about its mean.
- The exact half of the values are at the left to the center, and the exact half is at the right.
- The area under the curve is 1.
- The distribution can be described in terms of standard deviation and the mean.
Parameters of the Normal Distribution:
The normal distribution is calculated in two values: the mean and medium. These values determine the shape and probability of the distribution. The shape changes as the value of the parameters change.
The mean is a location parameter, while the standard deviation is a scale parameter. It means that the mean states the central point of the curve that determines the height of the curve. The standard deviation stretches the curve. A large standard deviation results in a stretched curve, while a small standard deviation results in a narrow curve.
Keynote: Changing the values of the parameters changes the size and shape of the bell curve. It does not mean that they change the shape of the graph completely.
Mean:
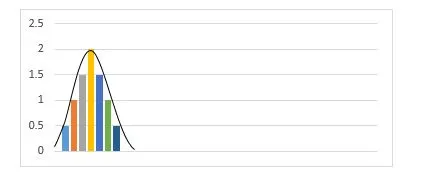
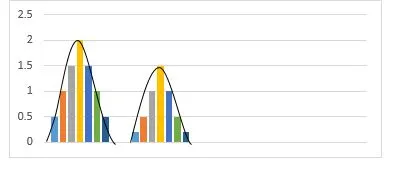
The mean is a measure of the central tendency. It can express the distribution of variables measured as ratios or intervals. In the normal distribution graph, the mean defines the peak. It is the point around which the remaining data points surround. Changing the value of the mean moves the curve to the left or right along the x-axis.
For example
Standard Deviation:
The standard deviation is the measure of the deviation of the data points from the mean. It estimates the distance between the data points and the mean. It determines at what distance the data points are located from the mean. The standard deviation on the graph determines the width of the curve. A small deviation results in a narrow and steep curve, while a large deviation results in a wide and flatter curve. As the value of standard deviation changes, the curve tightens or expands its width along the x-axis
Purpose of Normal Distribution:
The normal distribution is used commonly in natural and social science. The normal distribution is used commonly to express demographics and satisfaction, such as height, age, birth weight, blood pressure, marks on a test, workplace anxiety, reading aptitude, internet utility, etc.
Moreover, the central limit theorem defines the essentiality of the normal distribution and supports the base on how it works in the statistics. It states that the average of independent, identically distributed random variables form normal distributions, irrespective of the type of distribution.
Central Limit Theorem:
The central limit theory is a statistical theory that says that given a large sample size from a population with a defined variance, the mean of all samples from the population will be almost equal to the mean of the population. The samples will also follow an approximately normal distribution pattern. In simple words, if you add the means of all samples of a population and find the average, it will be approximately equal to the average of the same population.
Formula of Normal Curve:
F(x) = probability
X = the value of variable
µ = the mean
σ = standard deviation
σ2 = variance
π = 3.14159
e = 2.71828
Empirical rule:
The empirical rule tells you where the most of values lie in a normal distribution.
- About 95% of data points are within two standard deviations from the mean.
- About 68% of data points have a standard deviation of 1.
- Around more than 99% of data points are within three standard deviations from the mean.
Takeaways:
- A normal distribution is a technical term for the probability curve.
- There is symmetry about the center in a normal distribution.
- In the normal distribution mean=median=mode.
- The exact half of the values of the distribution are less than the mean, and the exact half is more than the mean.
FAQs About Normal Distribution
A normal distribution, also known as Gaussian distribution or probability density distribution, is a probability distribution that is symmetric about its mean, with data points near the mean.
There are two parameters of the normal distribution; the mean and standard deviation.
The central limit theorem is a statistical theorem that states that the average of independent, identically distributed random variables form normal distributions, irrespective of the type of distribution.