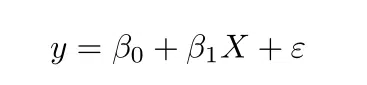Simple Linear Regression

What Simple Linear Regression (SLR) Means

In the simplest of terms, a simple linear regression is a statistical data technique where two quantitative values are plotted on a graph. The plot is a straight line, which means there’s a direct relationship between the two values. 

One value, ‘x,’ is called an independent (predictor or explanatory) variable, and the other, ‘y,’ is a dependent variable. Regression in this model represents the change occurring on a dependent variable as the independent one changes.

Examples:

• Effects of diet on an individual’s height (height = independent variable; diet = dependent variable). 
• Change in mental well-being based on monthly income in a specific area for a certain group of people (monthly income = independent variable; mental well-being = dependent variable). 

Pre-suppositions of SLR 

A research’s statistical data qualifies to be represented in the form of SLR, if and only if:

1. Normality: data is normally distributed.
2. Linearity: the relationship between the two variables is linear that is, one decreases, and so does the other, or vice versa. 
3. Homogeneity of variance aka homoscedasticity: values of the independent variable aren’t much affected/altered by the size of the error in predictions, no matter the size of that error.
4. Independence of observations: trust-worthy, valid, and accurate methods have been used to collect data; the data aren’t connected in some hidden way.

How to Form SLR Model using Formula – Method 1

At this point, you have all your data, the different numerals and what not. They need to be arranged depending on which value is x, y, and so on. These ‘labels’ the data needs to be categorized under are deduced from the following linear regression formula: 

Where:

• y = predicted value of the dependent variable  
• x = any given value of the independent variable 
• B0 = intercept, that is, predicted value of y when x = 0 or, in other words, the point where an estimated regression line will cross the y-axis
• B1 = regression coefficient, that is, the extent to which y is predicted to change as x changes
• e = error of estimate, that is, how much regression coefficient is expected to vary

Once you know which value is x, y, what counts as intercept, and so on, you can simply apply the above formula to calculate the regression. 

Tip: A simpler version of this formula, to calculate simple linear regression is: y = a + bx, where 

Y = dependent variable

X = independent variable 

b = slope of the line and 

a = y-intercept

How to Form SLR Model by Hand – Method 2

Apart from the above linear regression formula, you can also arrange your data and calculate regression by hand. To do so, follow these steps:

Step # 1 – Calculate the average of the x variable.

Step # 2 – Calculate the difference between each x and average x.

Step # 3 – Square the differences and add them all up. The resulting value will be ‘SSxx.’

Step # 4 – Calculate the average of the y variable.

Step # 5 – Multiply the differences of x and y from their respective averages. Then add them all up. The resulting value is ‘SSxy.’

Step # 6 – Using the two resulting values—SSxx and SSxy—calculate the intercept by subtracting SSxx / SSxy * average x from average y. 

Check out a simple example demonstrating the above steps, and it will all make much more sense!

How to Form SLR Model using Excel – Method 3

These days, organizing data in the SLR model has become super easy, thanks to Excel. There are also numerous, easy-to-understand visual demonstrations of how to plot data in a simple linear regression model using Excel.

Tip: Learn how to work with SLR in less than 15 minutes!

How to Form SLR Model Using Other Tools

Simple linear regression models are among the most commonly used models to represent research data. As such, there are many online SLR calculators, software, and other tools in place. They make the task of plotting data according to this model just as easy as Excel does. One of those tools is TI83.  

Interpreting and Representing Results

Representing results obtained via SLR includes and is based upon 3 components:

• estimated effect (i.e. the regression coefficient)
• standard error of the estimate
• p-value (probability value)

Once you have found out the regression coefficient via SLR, you can interpret it in words, which might look something like:

(Related to the second example mentioned above) “A significant relationship exists (p < 0.001) between monthly pay and mental well-being (R2 = 0.71 ± 0.018), with a 0.71-unit increase in reported mental well-being for every $10,000 increase in pay.”

Frequently Asked Questions