An Overview of the One-Way ANOVA
Published by at August 20th, 2021 , Revised On July 4, 2022
Analysis of Variance or ANOVA is a statistical test that uses the means of two or more groups to analyse the difference. A single independent variable is used by an ANOVA, while two independent variables are used in a two-way Anova.
An Example For a Crop Researcher:
As a researcher in the crop industry, he would possibly want to test 3 different fertiliser mixtures on the output or yield of a crop. He can use this test or One-way ANOVA to compare the results of the different combinations on his crop yields.
What is a One-way ANOVA Used For?
One way ANOVA has an independent variable and a dependent variable, where one is categorical, and one is quantitative. There are at least three levels of independent variables, such as different groups or categories.
Anova helps identify the impact of an independent variable over a dependent variable. This can be seen in the following:
- Social media usage of the independent variable and you delegate low medium, and high social media usages to classes to figure out whether consumers sleeping periods vary each night or not.
- The soda brand is an independent variable, and you gather statistics on Coke, Sprite, and Fanta to see if there is a price difference per 100ml.
- The independent variable is the fertiliser type and it uses mixtures 1, 2, and 3 to handle cropping fields to decide if the crop yield
In the null hypothesis (H0) the mean of the groups is not different. In the alternate hypothesis (Ha) at least one group is different from the accumulated mean of the dependent variable. The T-Test could be used for comparing two groups.
ANOVA Test
ANOVA decides how statistically the independent variable levels generate separate classes by determining whether the mean of the condition thresholds differs from the average mean of the dependent variable.
When either of the party terms varies significantly from the general mean, the null statement is rejected.
For statistical significance, ANOVA uses an F-test. It allows various approaches to be measured together since the error is determined for the whole range of comparisons rather than through a particular two-way comparison.
The F-test measures the deviation from the overall group variance in each mean sample. When the variation between groups is less than the variance between groups, a higher F-value would be observed in this F-test and thus the variation is more likely than the chance to be valid.
ANOVA Assumptions
The ANOVA test presuppositions are similar to the basic premises of every parametric test:
- Independence of observations: Statistically accurate methods have been used to gather the data, so there is no intimate relationship between observations. Using ANOVA for blocking variables if the results fail to fulfill this statement because you have a confounding variable for a statistically defined use.
- Usually distributed response variable: Dependent variable values are extended over a normal distribution.
- Homogeneity of variance: For each group the difference in each group is equal. When the variations between groups are substantial, ANOVA is not the best data match.
Using One-way ANOVA for Calculation
Although an ANOVA may be done by hand, when working with more than a few observations, it isn’t easy to do so. In the R Statistical System, we carry out our research because it is safe, efficient, and readily accessible. See our guide to conducting ANOVA in R for a complete overview of this ANOVA case.
In our hypothetical crop yield experiment, the sample dataset contains data:
- fertiliser type
- planting density
- planting location in the field
- final crop yield
This allows you to run many ANOVA experiments and test the setup best suited to the performance. We only analyse the effect of the fertiliser type on single-way ANOVA crop yield. The ANOVA command can be used, after loading the data set in our R method. In this situation, the difference in the mean variable of receptive output is modeled as a function of the fertiliser type.
Results Interpretation
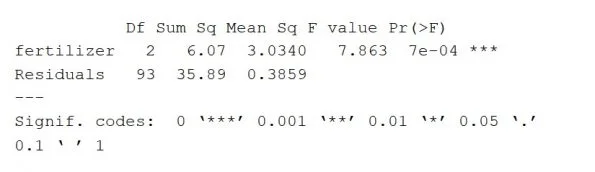
The ANOVA research summary (in R) appears as follows:
The performance of ANOVA gives an estimation of how much variance the dependent variable will compensate for. This displays the variable along with the residual test (including the model error).
The column Df shows the freedom degrees for the independent variable (called with the different levels of the index and 1 subtraction) and the freedom degrees (calculated with the cumulative sum of measurements minus 1 and the different levels of the different variables) for the residually measured variable.
The Sum Sq column indicates the square sum between the group values and the mean (also known as the total variation) that the indicator describes for this group. The sum of the fertiliser vector squares is 6.07, while the sum of the residual squares is 35.89.
The Mean square column is the value of the square sum, determined by dividing the square sum by the free classes.
The column of an F-value is the test results from the F-test: the average square for each independent variable separated by the average square. The bigger the F value the greater the variance with the independent variable is expected to be true and not chance-based.
The p-value of the F-statistic is the column Pr(>F). It indicates how likely it would have happened to the F-value measured on the study if the null hypothesis was correct that no distinction was made between community media.
According to its large p-value (p<0.05), the fertiliser form is estimated to have a major impact on the average crop yield. That is regardless of the p-value of the independent variable.
Post-hoc Testing
ANOVA will inform you that there are variations, but not major, between rates of the independent variable. A posthoc TukeyHSD (Tukey ‘s Honestly-Significant Difference) study is carried out to determine whether care conditions vary from each other.
The Tukey test measures each of the groups in pairs and uses a conservative error calculation to classify the statistically distinct groups.
Tukey test R code is TukeyHSD (one.way)
Tukey HSD output is given the following:
First and foremost, the model being tested will be reported then for the independent variable the pairwise differences among groups will be listed (‘Fit’).
The mean difference between each treatment with fertiliser (“diff”) and the lower and upper boundaries of the 95-per-cent confidence interval (‘lwr’ and ‘upr’) and the p-value adjustments for many pair-wise comparisons is seen in the $ fertiliser portion.
Comparisons reveal that the mean fertiliser type 3 yields are significantly higher than both fertiliser 1, 2, but there is not a statistically significant gap between average fertiliser yields 1, 2.
Reporting of ANOVA Results
If presenting the results of an ANOVA the following to be provided
- a summary of the variables,
- f-value,
- p-values of the independent variable,
- degrees of freedom,
- and description of results
For instance: Recording the effects of a one-way ANOVA, a statistically significant difference is observed in average crop yield as per fertiliser type ( f (2)= 9.073, p < 0.001).
A posthoc Tukey analysis showed major pair variations between fertiliser types 3 and 2, averaging 0.42 bushels per hectare (p <0.05), and averages 0.59 bushels/ hectare (p <0.01) of type 3 and 1 of fertilisers.