What Is Numerical Data, And What Are Its Types?

As far as mathematics is concerned, data is a collection of information. Most commonly, this data is to understand and evaluate a hypothesis in an experiment. Many types of data are used on different occasions and for different purposes to discuss a hypothesis. Numerical data is one of the most common and therefore of paramount importance in the mathematical world. This article will thoroughly discuss numerical data, why it is important, and its types.

What is Numerical Data?

Numerical data is a kind of data expressed in numbers. It is also sometimes referred to as quantitative data, which is always collected in numbers. In other words, numerical data is any data that contains measurable or calculable information. One attribute of the numerical data that differentiates it from other number form data types is that it is able to carry out arithmetic operations with the numbers.

Examples of Numerical Data:

Some of the types of numerical data include:

• Age
• Height
• Length
• Speed
• Weight
• IQ
• Number of movies watched
• Number of countries
• Number of smartphones users, etc.

Characteristics of Numerical Data:

1. Quantifiable:

The numerical data is called quantitative data as it has similar attributes to it. The numerical data is measurable and calculable therefore has quantitativeness.

2. Arithmetic Operation:

Arithmetic operations like addition and subtraction can be carried out on numerical data.

3. Interval Difference:

For every numerical data scale, it is essential to have equal intervals. Due to this interval difference, the arithmetic operations can be carried out on the data.

4. Data Visualisation:

The numerical data can be demonstrated visually in different ways. Numerical data can be presented in the form of histograms, dot plots, scatter plots, and stacked dot plots.

Importance of Numerical Data :

Numerical Data holds immense importance in research. It is because all statistical analysis is applicable while analyzing the numerical data. It also helps in making the research process easier. It provides the researcher with accurate information. As being able to be represented in diagrams, graphs, and charts, numerical data can help many businesses and industries monitor their progress and do competitor analysis.

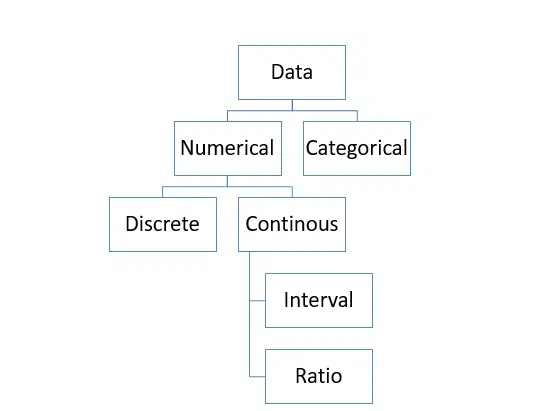
Types of Numerical Data:

Numerical data can be categorized into two groups:

1.   Discrete data:

Discrete data is a kind of numerical data that refers to countable items in a sample. It can take both numerical and categorical forms, depending on the situation and requirement. Therefore, discrete data can be counted or have a finite ending. It represents certain values of a list that can be finite or infinite. For example, it will represent numbers from, let’s say, 1- 100 or  1- infinity. Discrete data cannot be measured but counted, which means that it represents information categorized into a group. The number of employees in a company is an example of discrete data. While it is calculated, it cannot be measured.

Definition:

Discrete data is data that can only take certain values and is counted in whole numbers; the data variables cannot be subdivided into parts.

Tip: In most cases, discrete numbers are prefixed with ‘the number of.’ For example, the number of children, number of pushups, number of tulips, etc.

Examples of Discrete Data:

1. The number of Andriod users in the UK.
2. The number of vapers in the United States.
3. Number of cigarettes consumed regularly worldwide
4. The number of children of XYZ
5. The number of seats in parliament

Characteristics of Discrete data:

Discrete data is the most used data in all statistical analyses because they offer accurate and concrete information. Some of the key characteristics of discrete data include:

1. Discrete data comprises discrete variables that are countable, numeric, finite, and positive integers etc.
2. Discrete data can be numerical and categorical data—for example, the ethnicity of a person, gender, nationality, etc.
3. The values of discrete data cannot be subdivided.
4. The discrete data cannot be measured.
5. It is easy to demonstrate discrete data visually in the form of pie charts, line charts, and bar graphs.

2.   Continous Data:

Continuous data is another kind of numeric data that refers to an indefinite number of possible measurements between two realistic points. This data represents measurements; therefore, its values cannot be counted but measured. This data is about precision and accuracy; therefore, it also takes decimals with integers. This data is highly useful for researchers and examiners to get the most accurate information regarding a particular sample or population.

Definition:

Continuous data is measurable data that can be measured on an infinite scale. It can take numbers between two realistic numbers, no matter how small they are or if they are decimal numbers.

Examples:

1. Time in race
2. Distance from point A to B
3. Area of a field
4. Weight of a newborn
5. A person height
6. Cumulative Grade Point Average

You can divide the values of the above-mentioned examples into parts, and they will still be meaningful.

Characteristics of continuous data:

Some of the characteristics of continuous data are:

1. The continuous data is measurable but not countable
2. This kind of data changes over time and thus have different values at different intervals.
3. The continuous can or cannot consist of whole numbers.
4. The continuous data can be graphically represented in the form of bar graphs and skews etc.

The continuous data can be further divided into two categories:

1.    Interval:

Interval data is a kind of continuous numeric data that represents ordered values that have the same difference. It is a data type measured along a scale that contains equally spaced points. The values of interval data can be subtracted and added but cannot be divided or multiplied.

One of the examples of interval data could be CGPA. The mean of GPA is used to calculate the CGPA over different sessions with equal intervals.

Another example could be temperature:

-2, -1, 0, 1, 2

One thing to note is that this data does not have a true zero. Like with the temperature, the zero does not depict there is no temperature. Due to this particular attribute, many inferential and descriptive statistics cannot be applied.

Time is also an example of interval data as the numbers on the clock are measurable and equidistant from each other. The difference between each hour and minute is the same.

2.    Ratio:

The ratio is a type of continuous numerical data and is similar to interval data but has a real zero. The zero value of a variable depicts its literal meaning. For example, the speed of a car from point A to B can be 0 mph, 5 mph, 15 mph, 20 mph, and 25 mph. Apparently, it may look similar to the interval data, but it is not. 0 denotes that the car did not have any speed and therefore was at rest.

Unlike interval data, ratio data can be multiplied and divided.